EJEMPLO DE RESOLUCION DE UN EJERCICIO DE CICLO RANKINE

Una planta de vapor que sigue un Ciclo Rankine, opera ente las presiones de 20 MPa y 1 atm con el fin de generar energía eléctrica para una pequeña aglomeración urbana que require un apotencia de 10.000 kW. Para ello la municipalidad está dispuesta a invertir 30 millones de dólares por año en la operación de la planta.

Los detalles técnicos de la planta de vapor son:
- La caldera entrega vapor sobrecalentado a 35º C por sobre la temperatura de saturación.
- La turbina presenta un rendimiento de 80% y la bomba es considerada isoentrópica.
- El costo de cada kilogramo de vapor producido es de 0.05 USD
- La planta funcionaría 24 horas al día y 365 días por año.

Se desea saber si el proyecto es factible. Entregue su respuesta indicando el costo anual de funcionamiento de la planta y el rendimiento


DESARROLLO:

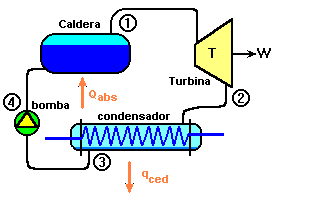
1. EN LA CONDICIÓN 1:

P1 = 20 MPa Tsat = 365.81ºC
(de tabla A-5 pág. A-13)

Entonces: T1 = Tsat + 35ºC ˜ 400ºC

Por lo tanto: h1 = hvs (20 MPa, 400ºC) = 2818.1 kJ/kg
s1 = svs (20 MPa, 400ºC) = 5,554 kJ/kg

Considerando la turbina como un dispositivo isoentrópico

s1 = s2 = 5,554 kJ/kg

Además se sabe que: p2 = 1 atm ˜ 0.1 MPa = 100 kPa

Entonces: Tsat (0.1 MPa) = 99,63ºC (tabla A-5 pág. A-12)
svs (0.1 MPa) = 7,3594 kJ/kg (tabla A-5 pág. A-12)
sls (0.1 MPa) = 1,3026 kJ/kg (tabla A-5 pág. A-12)

Ahora estamos en condiciones de obtener el título del vapor, así:

s2 = 5,554 = 7,3594 X’2 + 1,3026 (1-X’2)

despejando, se tiene: X’2 = 0,702

con esto podemos obtener que:

h’2 = hvs(0,1 MPa) X’2 + hls(0,1 MPa) (1- X’2 ) (valores de hvs y hls obtenidos de tabla
A-5 pág. A-12)
= 2675,5 x 0.702 + 417,46 x (1 - 0,702)
h’2 = 2002,6 kJ/kg

Entonces:

W’T = h2 – h1 = 2002,6 - 2818,1
W’T = -815.5 kJ/kg (teórico)

Recordando que: Rend.T = W’real / W’teórico

Reemplazando valores conocidos: 0,8 = W’Real / -815,5 kJ/kg

Entonces: W’Real = -652,4 kJ/kg

Finalmente: h2 = h1 – 652,4
= 2818,1 – 652,4

h2 = 2165,7 kJ/kg

2. EN LA CONDICIÓN 3:

Estamos en presencia de un líquido saturado a presión de 1 atmósfera.
Entonces:
h3 = hls (0.1 MPa) = 417,46 kJ/kg (tabla A-5 pág. A-12)

Por lo tanto: qf = h3 - h2 = 417,46 – 2165,7 =

qf = -1748,24 kJ/kg

3. PARA LA BOMBA:

W’B = h4 – h3 ˜ vls*dp; dp: diferencia de presión a través de la bomba

De tabla A-5 pág. A-12: vls (0,1 MPa) = 0,001043 m3/kg
h3 = hls (0,1MPa) = 417.46 kJ/kg

Además: p4 = 0,1 MPa = 100 kPa
p3 = 20 MPa = 20.000 kPa

Entonces: W’B = (0,001034m3/kg) x (20.000 kPa – 100 kPa)
W’B = 20,756 kJ/kg

y: h4 = h3 + W’B = 417,46 kJ/kg + 20,756 kJ/kg
h4 = 438,22 kJ/kg

Por lo tanto: qc = h1 – h4 = 2818,1 – 438,22

qc = 2379,88 kJ/kg

COSTO ANUAL DE LA PLANTA:

Requerimientos: Potencia (P) = 10.000 kW ó 10.000 kJ/s

Obteniendo de la cantidad o flujo de vapor (mv) que circula por la turbina:

mV = P / WReal = 10.000 kJ/s / 652.4 kJ/kg

mv = 15.33 kg/s

Entonces el costo anual se calcula:

Costo anual = (mv) x (0.05 USD/kg de vapor) x (3600 s/h) x (24 h/día) x (365 días/año)
= 15.33 x 0.05 x 3600 x 24 x 365

Costo anual = 24.172.344 USD/año Por lo tanto el proyecto es factible de realizarse ya que la municipalidad está dispuesta a gastar 30 millones de dólares por año lo que supera el costo real del funcionamiento de la planta.

RENDIMIENTO DEL CICLO:

Rendimiento del Ciclo = (¦WReal¦ - ¦WBomba¦) / qc

= ( 652,4 – 20,756) / 2379,88

Rendimiento del Ciclo = 0,265 o 26.5%